C: y=x^2 上に 点A,B があり, 線分AB と C で囲まれる面積が常に 1/6 であるものとする。このとき 直線AB が通過しうる範囲を図示せよ。
要するに 直線y=(2a+1)x-a^2-a の通過範囲を示せということらしいです。
パソコンに描いてもらいました。
aの値を-6.25から6.25まで変化させています。
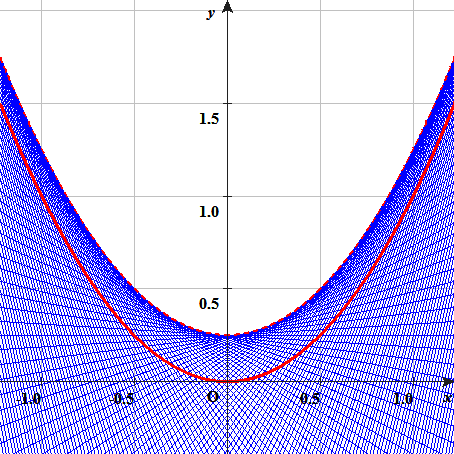
赤実線―― C
赤点線―― y=x^2+1/4
一目瞭然。
便利な世の中になりましたけど、直線の式まで変形したのは人間です。
何でも頼ってたら、それこそ計算する意味すらどこかに飛んでしまいかねない。
翻訳機能を持ったサイト(このページのサイドバーにもボックスはありますが)など見ていても、つくづくそう思います。